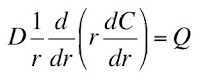| Online: | |
| Visits: | |
| Stories: |

| Story Views | |
| Now: | |
| Last Hour: | |
| Last 24 Hours: | |
| Total: | |
The Number and Distribution of Capillaries in Muscles with Calculations of the Oxygen Pressure Head Necessary for Supplying the Tissue
Oxygen diffuses from capillaries into tissue where it is used for metabolism. Russ Hobbie and I discuss diffusion in Chapter 4 of Intermediate Physics for Medicine and Biology. Below is a new homework problem on this topic.
Section 4.11Problem 37 ½. Consider a cylindrical capillary of radius a, containing blood having an oxygen concentration Co (molecules/m3). The capillary is surrounded by a cylinder of tissue of radius b that has an oxygen concentration C(r), consumes oxygen at a rate per unit volume Q (molecules/m3s), and has a diffusion constant D (m2/s). At r = a, C = Co and at r = b, dC/dr = 0. Within the tissue, C(r) obeys the steady-state diffusion equation
(a) Calculate C(r). Hint: guess a solution of the form C(r) = A + B r2 + E ln(r), and determine values for the constants A, B, and E.
(b) Plot C(r) versus r assuming b = 10a and Qb2/(CoD) = 1
(c) Determine the minimum value of Co as a function of a, b, D, and Q, assuming the oxygen concentration is nowhere negative.
(d) Describe what assumptions underlie this model.
This problem plays an important role in the history of physiology. August Krogh used the model to infer that when Q increased during exercise, b must decrease (by additional vessels opening that were closed when the muscle was at rest) in order to supply the tissue with sufficient oxygen. For “his discovery of the capillary motor regulating mechanism,” he was awarded the Nobel Prize. Krogh’s model also represents an early contribution of mathematical modeling to medicine and biology. He presented his model in the paper:
Krogh, A. (1919) The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J. Physiol., 52: 409-415.
He acknowledges mathematician K. Erlang for deriving the mathematical formula for C(r).
Isaac Asimov includes an entry for Krogh in Asimov’s Biographical Encyclopedia of Science and Technology (Second Revised Edition).
KROGH, Schack August Steenberg (krawg)
Danish physiologist
Died: Copenhagen, September 13, 1949
Krogh, the son of a brewer, was educated at the University of Copenhagen, where he intended to study medicine but shifted his interest to physiology. He obtained his master’s degree in 1899.
He was particularly involved in respiration, following the path of oxygen, nitrogen, and carbon dioxide in and out of the body. In 1908 he gained a professorial position at the University of Copenhagen and there his studies of respiration led him to suggest that the capillaries (the tiniest blood vessels) of the muscles were open during muscular work and partially closed during rest. He went on to demonstrate this and to show the importance of such capillary control to the economy of the body.
For this work, he was awarded the Nobel Prize in Physiology and Medicine in 1920. He went on thereafter to show that this capillary control was brought about by the action of both muscles and hormones.
After Denmark was occupied by Nazi Germany in 1940, Krogh was forced to go underground and then to escape to Sweden. He remained there till the end of the war, then returned to liberated Denmark.
Source: http://hobbieroth.blogspot.com/2016/01/the-number-and-distribution-of.html